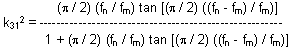Because a piezoelectric ceramic is anisotropic, physical constants relate to both the direction of the applied mechanical or electric force and the directions perpendicular to the applied force. Consequently, each constant generally has two subscripts that indicate the directions of the two related quantities, such as stress (force on the ceramic element / surface area of the element) and strain (change in length of element / original length of element) for elasticity. The direction of positive polarization usually is made to coincide with the Z-axis of a rectangular system of X, Y, and Z axes (Figure 1.6). Direction X, Y, or Z is represented by the subscript 1, 2, or 3, respectively, and shear about one of these axes is represented by the subscript 4, 5, or 6, respectively. Definitions of the most frequently used constants, and equations for determining and interrelating these constants, are summarized here. The piezoelectric charge constant, d, the piezoelectric voltage constant, g, and the permittivity, e, are temperature dependent factors.
Figure 1.6 – The direction of positive polarization usually is made to coincide with the Z-axis.
Piezoelectric Charge Constant
The piezoelectric charge constant, d, is the polarization generated per unit of mechanical stress (T) applied to a piezoelectric material or, alternatively, is the mechanical strain (S) experienced by a piezoelectric material per unit of electric field applied. The first subscript to d indicates the direction of polarization generated in the material when the electric field, E, is zero or, alternatively, is the direction of the applied field strength. The second subscript is the direction of the applied stress or the induced strain, respectively. Because the strain induced in a piezoelectric material by an applied electric field is the product of the value for the electric field and the value for d, d is an important indicator of a material’s suitability for strain-dependent (actuator) applications.
| d33 | induced polarization in direction 3 (parallel to direction in which ceramic element is polarized) per unit stress applied in direction 3 or induced strain in direction 3 per unit electric field applied in direction 3 |
|---|---|
| d31 | induced polarization in direction 3 (parallel to direction in which ceramic element is polarized) per unit stress applied in direction 1 (perpendicular to direction in which ceramic element is polarized) or induced strain in direction 1 per unit electric field applied in direction 3 |
| d15 | induced polarization in direction 1 (perpendicular to direction in which ceramic element is polarized) per unit shear stress applied about direction 2 (direction 2 perpendicular to direction in which ceramic element is polarized) or induced shear strain about direction 2 per unit electric field applied in direction 1 |
Piezoelectric Voltage Constant
The piezoelectric voltage constant, g, is the electric field generated by a piezoelectric material per unit of mechanical stress applied or, alternatively, is the mechanical strain experienced by a piezoelectric material per unit of electric displacement applied. The first subscript to g indicates the direction of the electric field generated in the material, or the direction of the applied electric displacement. The second subscript is the direction of the applied stress or the induced strain, respectively. Because the strength of the induced electric field produced by a piezoelectric material in response to an applied physical stress is the product of the value for the applied stress and the value for g, g is important for assessing a material’s suitability for sensing (sensor) applications.
| g33 | induced electric field in direction 3 (parallel to direction in which ceramic element is polarized) per unit stress applied in direction 3 or induced strain in direction 3 per unit electric displacement applied in direction 3 |
|---|---|
| g31 | induced electric field in direction 3 (parallel to direction in which ceramic element is polarized) per unit stress applied in direction 1 (perpendicular to direction in which ceramic element is polarized) or induced strain in direction 1 per unit electric displacement applied in direction 3 |
| g31 | induced electric field in direction 1 (perpendicular to direction in which ceramic element is polarized) per unit shear stress applied about direction 2 (direction 2 perpendicular to direction in which ceramic element is polarized) or induced shear strain about direction 2 per unit electric displacement applied in direction 1 |
Permittivity Constant
The permittivity, or dielectric constant, ε, for a piezoelectric ceramic material is the dielectric displacement per unit electric field. εT is the permittivity at constant stress, εS is the permittivity at constant strain. The first subscript to ε> indicates the direction of the dielectric displacement; the second is the direction of the electric field.
The relative dielectric constant, K, is the ratio of , the amount of charge that an element constructed from the ceramic material can store, relative to the absolute dielectric constant, 0 , the charge that can be stored by the same electrodes when separated by a vacuum, at equal voltage (0 = 8.85 x 10-12 farad / meter).
| εT11 | :permittivity for dielectric displacement and electric field in direction 1 (perpendicular to direction in which ceramic element is polarized), under constant stress |
| εS33 | :permittivity for dielectric displacement and electric field in direction 3 (parallel to direction in which ceramic element is polarized), under constant strain |
Elastic And Compliance
Elastic compliance, s, is the strain produced in a piezoelectric material per unit of stress applied and, for the 11 and 33 directions, is the reciprocal of the modulus of elasticity (Young’s modulus, Y). sD is the compliance under a constant electric displacement; sE is the compliance under a constant electric field. The first subscript indicates the direction of strain, the second is the direction of stress.
| sE11 | elastic compliance for stress in direction 1 (perpendicular to direction in which ceramic element is polarized) and accompanying strain in direction 1, under constant electric field (short circuit) |
|---|---|
| sD33 | elastic compliance for stress in direction 3 (parallel to direction in which ceramic element is polarized) and accompanying strain in direction 3, under constant electric displacement (open circuit) |
Young’s Modulus
Young’s modulus, Y, is an indicator of the stiffness (elasticity) of a ceramic material. Y is determined from the value for the stress applied to the material divided by the value for the resulting strain in the same direction.
Electromechanical Coupling Factor
The electromechanical coupling factor, k, is an indicator of the effectiveness with which a piezoelectric material converts electrical energy into mechanical energy, or converts mechanical energy into electrical energy. The first subscript to k denotes the direction along which the electrodes are applied; the second denotes the direction along which the mechanical energy is applied, or developed.
k values quoted in ceramic suppliers’ specifications typically are theoretical maximum values. At low input frequencies, a typical piezoelectric ceramic can convert 30 – 75% of the energy delivered to it in one form into the other form, depending on the formulation of the ceramic and the directions of the forces involved.
A high k usually is desirable for efficient energy conversion, but k does not account for dielectric losses or mechanical losses, nor for recovery of unconverted energy. The accurate measure of efficiency is the ratio of converted, useable energy delivered by the piezoelectric element to the total energy taken up by the element. By this measure, piezoelectric technology in well designed systems can exhibit efficiencies that exceed 90%.
The dimensions of a ceramic element can dictate unique expressions of k. For a thin disc of piezoelectric ceramic the planar coupling factor, kp , expresses radial coupling – the coupling between an electric field parallel to the direction in which the ceramic element is polarized (direction 3) and mechanical effects that produce radial vibrations, relative to the direction of polarization (direction 1 and direction 2). For a disc or plate of material whose surface dimensions are large relative to its thickness, the thickness coupling factor, kt , a unique expression of k33 , expresses the coupling between an electric field in direction 3 and mechanical vibrations in the same direction. The resonance frequency for the thickness dimension of an element of this shape is much higher than the resonance frequency for the transverse dimensions. At the same time, strongly attenuated transverse vibrations at this higher resonance frequency, a result of the transverse contraction / expansion that accompanies the expansion / contraction in thickness, make kt lower than k33 , the corresponding factor for longitudinal vibrations of a thin rod of the same material, for which a much lower longitudinal resonance frequency more closely matches the transverse resonance frequency.
| k33 | factor for electric field in direction 3 (parallel to direction in which ceramic element is polarized) and longitudinal vibrations in direction 3 (ceramic rod, length >10x diameter) |
|---|---|
| kt | factor for electric field in direction 3 and vibrations in direction 3 (thin disc, surface dimensions large relative to thickness; kt < k33) |
| k31 | factor for electric field in direction 3 (parallel to direction in which ceramic element is polarized) and longitudinal vibrations in direction 1 (perpendicular to direction in which ceramic element is polarized) (ceramic rod) |
| kp | factor for electric field in direction 3 (parallel to direction in which ceramic element is polarized) and radial vibrations in direction 1 and direction 2 (both perpendicular to direction in which ceramic element is polarized) (thin disc) |
Dielectric Dissipation Factor
The δ, tan δ, for a ceramic material is the tangent of the dielectric loss angle. tan δ is determined by the ratio of effective conductance to effective susceptance in a parallel circuit, measured by using an impedance bridge. Values for tan δ typically are determined at 1 kHz.
Piezoelectric Frequency Constant
When an unrestrained piezoelectric ceramic element is exposed to a high frequency alternating electric field, an impedance minimum, the planar or radial resonance frequency, coincides with the series resonance frequency, fs. The relationship between the radial mode resonance frequency constant, NP , and the diameter of the ceramic element, DΦ , is expressed by:
NP = fs DΦ
At higher resonance, another impedance minimum, the axial resonance frequency, is encountered. The thickness mode frequency constant, NT , is related to the thickness of the ceramic element, h, by:
NT = fs h
A third frequency constant, the longitudinal mode frequency constant, is related to the length of the element:
NL = fs l
Most-Used Constants and Equations
Aging Rate
Aging rate = (Par2 – Par1) / ((Par1) (log t2 – log t1))
Bandwidth
B ≡ kfp or B ≡ kfs
Dielectric Constant (Relative)
permittivity of ceramic material / permittivity of free space*
KT = εT / <ε0
*8.85 x 10-12 farad / meter
Dielectric Dissipation Factor (Dielectric Loss Factor)
conductance / susceptance for parallel circuit equivalent to ceramic element;
tangent of loss angle (tan d)
measure directly, typically at 1 kHz
Elastic Compliance
strain developed / stress applied;
inverse of Young’s modulus (elasticity)
s = 1 / ν2
sD33 = 1 / YD33
sE33 = 1 / YE33
sD11 = 1 / YD11
sE11 = 1 / YE11
Electromechanical Coupling Factor
mechanical energy converted / electric energy input
or
electric energy converted / mechanical energy input
Static / low frequencies
ceramic plate
k312 = d312 / (sE11εT33 )
ceramic disc
kp2 = 2d312 / ((sE11 + sE12)εT33 )
ceramic rod
k332 = d332 / (sE33εT33 )
Higher frequencies
ceramic plate
ceramic disc
kp ≅ √ [(2.51 (fn – fm) / fn) – ((fn – fm) / fn)2]
ceramic rod
k332 = (π / 2) (fn / fm) tan [(π / 2) ((fn – fm) / fn)]
any shape
keff2 = (fn2 – fm2 ) / fn2
Frequency Constant
resonance frequency o linear dimension governing resonance
NL (longitudinal mode) = fs l
NP (radial mode) = fs DΦ
NT (thickness mode) = fs h
Mechanical Quality Factor
reactance / resistance for series circuit equivalent to ceramic element
Qm = fn2 / (2πfm C0 Zm (fn2 – fm2))
Piezoelectric Charge Constant
electric field generated by unit area of ceramic / stress applied
or
strain in ceramic element / unit electric field applied
d = k√(sEεT )
d31 = k31√(sE11εT33 )
d33 = k33√(sE33εT33 )
d15 = k15E55εT11 )
Piezoelectric Voltage Constant
electric field generated / stress applied
or
strain in ceramic element / electric displacement applied
g = d / εT
g31 = d31 / εT33
g33 = d33 / εT33
g15 = d15 / εT11
Young’s Modulus
stress applied / strain developed
Y = (F / A) / (Δl / l) = T / S
Relationship among d, εT, and g
g = d / εT or d = gεT
Symbols
| A | surface area of ceramic element (m2 ) |
| B | bandwidth (frequency) |
| d | piezoelectric charge constant (C / N) |
| DΦ | diameter of ceramic disc or rod (m) |
| ε0 | permittivity of free space (8.85 x 10-12 farad / m) |
| εT | permittivity of ceramic material (farad / m) (at constant stress |
| F | force |
| fm | minimum impedance frequency (resonance frequency) (Hz) |
| fn | maximum impedance frequency (anti-resonance frequency) (Hz) |
| fp | parallel resonance frequency (Hz) |
| fs | series resonance frequency (Hz) |
| g | piezoelectric voltage constant (Vm / N) |
| h | height (thickness) of ceramic element (m) |
| k | electromechanical coupling factor |
| keff | effective coupling factor |
| KT | relative dielectric constant (at constant stress) |
| l | initial length of ceramic element (m) |
| N | frequency constant (Hz*m) |
| Par1 | value for parameter Par at t1 (days) |
| Par2 | value for parameter Par at t2 (days) |
| Qm | mechanical quality factor |
| ρ | density of ceramic (kg / m3 ) |
| s | elastic compliance (m2 / N) |
| S | strain |
| t1 | time 1 after polarization (days) |
| t2 | time 2 after polarization (days) |
| tan δ | dielectric dissipation factor |
| T | stress |
| To | temperature |
| TC | Curie point (°C) |
| ν> | velocity of sound in the ceramic material (m / s) |
| w | width of ceramic element (m) |
| Y | Young’s modulus (N / m2 ) |
| Zm | minimum impedance at fm (ohm) |